数据结构笔记

这学期感觉 Terry 的 Data Structures for Application Developers 对我帮助巨大。毕竟非科班出身，很多概念都是一知半解。第一天上课的时候，Terry 掏出了一把小锤子，尝试用它干各种事情。大家哈哈大笑的时候，Terry 说，

This is exactly what you are doing. You have lots of tools, but you always use ArrayList.

这门课学下来，Terry 深入浅出地讲解了各种基础算法和数据结构、它们背后的实现、以及如何去选择，上完课的时候真的让我有些醍醐灌顶的感觉。最后一节课下课前，Terry 又说，

Now you know your tools. Use them wisely.

这里就来梳理一下我们手中的 tools。

Array, ArrayList, LinkedList

Array 与 Linear Search

Java 中的数组（没记错的话 C 也是）长度是固定的，即数组一旦创建无法改变大小，所以数组的 length 是 immutable field。如果需要改变，只能创建一个新的更大的数组然后调用 System.arraycopy() 复制。在内存中，假设我们有数组 int array[]，其中 array[0] 的地址是 0x200，那么 array[2] 的地址就是 0x200 + 2 * 4（Java 中 int 是 4 bytes）= 0x208，因此通过下标获取数组中的某个元素可以在常数时间内完成（直接计算地址）。如果用 C 表示的话，那就是 array[2] 和 *(array + 2) 是完全一样的。

假设我们需要在 Array 中找到一个值并删除，一种简单的思路当然是遍历数组总会找到的，这就是 linear search 或 sequential search，一种最简单的搜索算法。同时，在 worst-case 下，它的运行时间也是 O(n) 的，因为可能需要遍历所有 n 个元素。

ArrayList 与 Binary Search

Java 中的 ArrayList 提供了诸如 add()，set() 一类的操作，看起来像是能够改变数组的长度。实际上，ArrayList 底层有一个 Array 数据结构，在每次执行 add() 方法前，会先执行 ensureCapacity() 方法去确保当前持有的 Array 能够有足够的空间。如果没有的话，ArrayList 会创建一个新的更大的数组，然后把旧数组的所有内容复制过来。

public void ensureCapacity(int minCapacity) {
    modCount++;
    int oldCapacity = elementData.length;
    if (minCapacity > oldCapacity) {
        Object oldData[] = elementData;
        int newCapacity = (oldCapacity * 3) / 2 + 1;
        if (newCapacity < minCapacity) {
            newCapacity = minCapacity;
        }
        elementData = Arrays.copyOf(elementData, newCapacity);
    }
}

注意在计算 newCapacity 时的 + 1，这是为了保证在 oldCapacity == 0 的时候也能够按照我们预期的执行。

因此，ArrayList 频繁执行 add() 会造成时间复杂度显著的增加，原因在于一般情况下 add() 可以在常数时间完成，然而一旦触发数组复制，需要消耗和原数组长度线性相关的时间去执行复制。因此，不断调用 ArrayList 的 add()，消耗的时间曲线类似于这样：

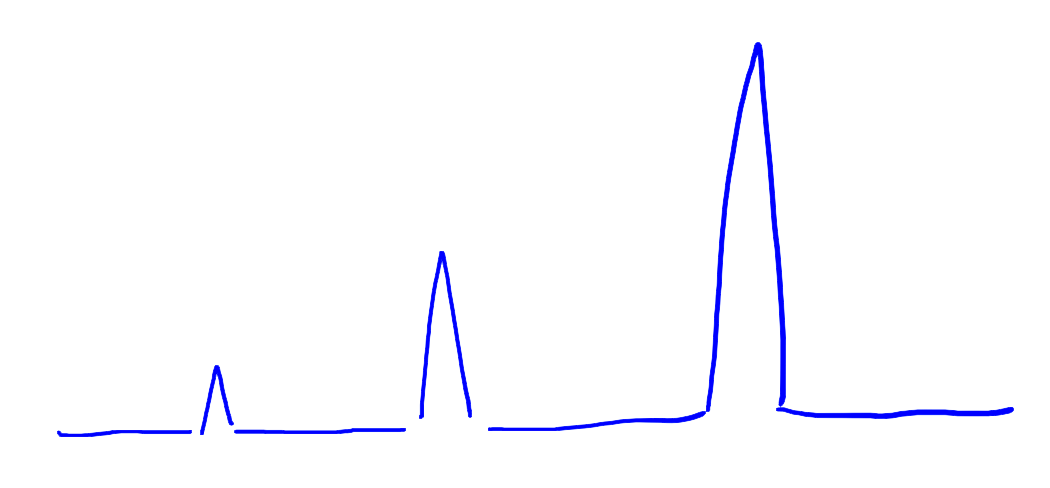
这就是 ArrayList 的 latency issue。还要注意，在调用 remove() 的时候，由于 Array 不允许内部出现空，因此 ArrayList 需要把内部数组里待删除元素之后的元素全部左移，而且不像 add() 仅会在特定次数时触发数组复制，每次 remove() 都会导致元素移动，因此是非常效率低下的。

对于一个排好序的数组，除了 linear search，一个更好的选择是 binary search。它的思路是每次比较数组正中间的值，如果大于中间值，则对右半边数组继续搜索，否则在左半边搜索。Binary search 大大减少了搜索所需要的时间复杂度，可以达到 O(log n)。

func binarySearch(data: [Int], key: Int) -> Int {
    guard !data.isEmpty else {
        return NSNotFound
    }

    var lowerBound = 0
    var upperBound = data.count - 1
    var mid = 0

    while true {
        if lowerBound > upperBound {
            return NSNotFound
        }
        // 注意：直接使用 (lowerBound + upperBound) / 2 可能导致超出 Int 范围溢出
        mid = lowerBound + (upperBound - lowerBound) / 2
        if data[mid] == key {
            return mid
        } else if data[mid] < key {
            lowerBound = mid + 1
        } else {
            upperBound = mid - 1
        }
    }
}

LinkedList

为了在常数时间内执行 add() 和 remove()，我们提出了 LinkedList 的数据结构。LinkedList 的思想是：一条链表由若干节点构成，每个节点的 next 属性指向它的下一个节点，链表的 head 指向第一个节点，这就是 singly linked list。如果节点还具有 prev 属性指向它的上一个节点，链表还具有 tail 属性指向最后一个节点，这就是一个 doubly linked list。

实现 LinkedList 的数据结构。首先我们需要定义节点的类，把它实现为一个 inner class。

class LinkedList<T: Equatable> {

    private(set) var head: Node<T>?

    init() {
        self.head = nil
    }

    class Node<T> {
        var data: T
        var next: Node<T>?

        init(data: T, next: Node<T>? = nil) {
            self.data = data
            self.next = next
        }
    }

}

然后实现 SinglyLinkedList 的各个方法。这里如果我们需要插入一个元素，只要找到上一个元素，然后更改对应的引用就可以了；删除同理。因此，链表的插入和删除可以较快完成。同样的，链表并不是连续的数据结构，一个链表的相邻节点可以在内存中相隔很远。

// 添加到链表开头
func addFirst(_ item: T) {
    let newHead = Node(data: item, next: head)
    head = newHead
}

// 添加到链表结尾
func addLast(_ item: T) {
    guard let head else {
        addFirst(item)
        return
    }

    var tmp = head
    while let next = tmp.next {
        tmp = next
    }
    tmp.next = Node(data: item)
}

// 在后面插♂入
func insert(after key: T, item: T) {
    var tmp = head
    while tmp != nil, tmp?.data != key {
        tmp = tmp?.next
    }
    tmp?.next = Node(data: item, next: tmp?.next)
}

// 在前面插入
func insert(before key: T, item: T) {
    guard let head else {
        return
    }

    if head.data == key {
        addFirst(item)
        return
    }

    var prev: Node<T>?
    var curr: Node<T>? = head

    while curr != nil, curr?.data != key {
        prev = curr
        curr = curr?.next
    }

    if let curr {
        prev?.next = Node(data: item, next: curr)
    }
}

// 删除
func remove(_ item: T) {
    guard let head else {
        return
    }

    if head.data == item {
        self.head = head.next
        return
    }

    var prev: Node<T>?
    var curr: Node<T>? = head

    while curr != nil, curr?.data != item {
        prev = curr
        curr = curr?.next
    }

    if let curr {
        prev?.next = curr.next
    }
}

总结

• Array 或 ArrayList
  • 随机访问的数据结构：每一项可以在常数时间内获取
  • 插入和删除时需要消耗大量资源（移位，复制），连续的数据结构
• LinkedList
  • 顺序访问的数据结构：元素只能按照一定顺序访问（next, prev）
  • 链表元素持有数据和对下一个（上一个）元素的引用
  • 插入和删除元素时无需移动元素，只需要更改引用，不连续的数据结构

Stack, Queue

Stack

栈是一种按照后入先出（last-in-first-out, aka LIFO）顺序插入/移除元素的数据结构。栈的使用非常普遍，例如浏览器的历史记录，例如 iOS 中 UINavigationController 就是维护了一个栈。栈最关键的是有两种操作（peek 不关键）：

• Push：把一个元素压到栈顶
• Pop：把栈顶的元素弹出
• Peek：返回栈顶元素，无需弹出

栈是建立在其它数据结构的基础上的，它的内部可以是数组也可以是链表。比如，我们可以用一个 LinkedList 去实现栈，这样 push 操作可以用 addLast()，pop 操作可以用 removeLast()。栈的 push 和 pop 操作都应该在常数时间内完成。

基于 Swift Array，栈可以非常简单地实现。

class Stack<T> {

    private var array: [T]

    init() {
        self.array = []
    }

    var isEmpty: Bool {
        array.isEmpty
    }

    func push(_ item: T) {
        array.append(item)
    }

    @discardableResult
    func pop() -> T? {
        return array.popLast()
    }

    func peek() -> T? {
        return array.last
    }

}

Queue

队列是一种按照先入先出（first-in-first-out, aka FIFO）顺序插入/移除元素的数据结构。队列也非常常见，比如打印机的队列、在星巴克门店的排队。队列主要也有两种操作：

• Enqueue：把一个元素插入到队列的尾部
• Dequeue：把队首元素移除

队列也可以建立在其他数据结构基础上，最简单的当然还是 LinkedList，入队即是 addLast()，出队即 removeFirst()。同样的，入队和出队操作也应该在常数时间内完成。

这里给一个基于 Swift Array 的非常简单的队列实现。

class Queue<T> {

    private var array: [T]

    init() {
        self.array = []
    }

    var isEmpty: Bool {
        array.isEmpty
    }

    func enqueue(_ item: T) {
        array.append(item)
    }

    @discardableResult
    func dequeue() -> T? {
        if isEmpty {
            return nil
        }
        let first = array.first
        array.remove(at: 0)
        return first
    }

    func peekFront() -> T? {
        return array.first
    }

}

HashTable

Hashing

哈希表的主要目标是提高搜索的速度。回想之前总结的，linear search 可以保证 O(n) 的运行速度，而对一个排好序的数组，binary search 可以达到 O(log n) 的运行速度。在数组中，我们知道根据下标访问元素是 O(1) 的，那么如果我们知道要搜索的值所对应的下标，则搜索速度也将被加快到 O(1)。用来把搜索值和下标对应起来的函数就是哈希函数。一个良好的哈希函数应该有以下特点：

• 能够快速计算
• 在下标范围内均匀分布

假设我们的哈希函数是取 4 的余数，这样对于 5 和 65 我们会得到相同的哈希值 1。对不同元素计算出相同哈希值叫做发生了 collision（碰撞？），解决 collision 主要有以下方法：

• Open addressing
  • Linear probing：发生 collision 后，直接继续向下找，直到找到数组中一个空的地方可以存放数据。需要注意的是，由于数组长度是不可变的，因此我们定义一个概念叫做 load factor（元素个数/数组长度），如果 load factor 超过某个阈值，我们就创建一个更大的数组，重新计算哈希值并排列元素。
  • Quadratic probing：利用一个固定的步长去做 secondary clustering。
  • Double hashing：首先计算哈希值，其次利用哈希值计算步长。通常使用的公式是 s = 1 + (k % (m−2))，其中 s 为步长，k 为第一步计算的哈希值，m 为数组长度。
• Closed addressing
  • Separate chaining：对于每一个哈希值，不再指向数组中确定的值，而是指向一个链表，具有相同哈希值的元素均存储在哈希值对应的链表中。

HashTable

我们根据 linear probing 来处理 collision，用数组作为哈希表的底层数据结构。首先实现哈希表数据结构和 inner class：

class HashTable {
    // inner class
    class DataItem {
        let key: Int
        init(key: Int) {
            self.key = key
        }
    }

    private var hashArray: [DataItem?]

    init(initialCapacity: Int) {
        self.hashArray = Array(repeating: nil, count: initialCapacity)
    }

}

然后我们实现关键的哈希函数，这里我们简单地使用取模。

private func hash(_ key: Int) -> Int {
    return key % hashArray.count
}

接下来我们实现搜索、删除和插入，核心思路都是计算 key 的哈希值，如果不对就继续向下找。

// 搜索
func search(_ key: Int) -> Bool {
    var hashVal = hash(key)
    while hashArray[hashVal] != nil {
        if hashArray[hashVal]?.key == key {
            return true
        }
        hashVal += 1
        // 每次都取模防止溢出
        hashVal %= hashArray.count
    }
    return false
}

// 删除
@discardableResult
func delete(_ key: Int) -> Int {
    var hashVal = hash(key)
    while let dataItem = hashArray[hashVal] {
        if dataItem.key == key {
            hashArray[hashVal] = nil
            return key
        }
        hashVal += 1
        hashVal %= hashArray.count
    }
    return NSNotFound
}

// 插入
func insert(key: Int) {
    let item = DataItem(key: key)
    var hashVal = hash(key)
    while hashArray[hashVal] != nil {
        hashVal += 1
        hashVal %= hashArray.count
    }
    hashArray[hashVal] = item
}

Binary Tree

啥是二叉树

我们知道，在排好序的数组中，binary search 可以达到 O(log n) 的搜索速度，但插入和删除很慢。在 LinkedList 中可以达到 O(1) 的插入和删除速度，但需要 O(n) 去搜索。如何把两种数据结构的优点结合起来呢？答案就是树，这里我们具体讨论二叉树。

一棵树具有以下结构：

• Root：树顶端的节点。
• Parent：当一个节点（除了根）具有一条向上的边连接另一个节点时，这里上面的节点就称为父节点。
• Child：同上，下面那个节点就称为子节点。
• Leaf：没有任何子节点的节点称为叶。一棵树中只有一个根，但可以有很多个叶节点。
• Level/Height：一个节点到树的根的层级数称为这个节点的 level。

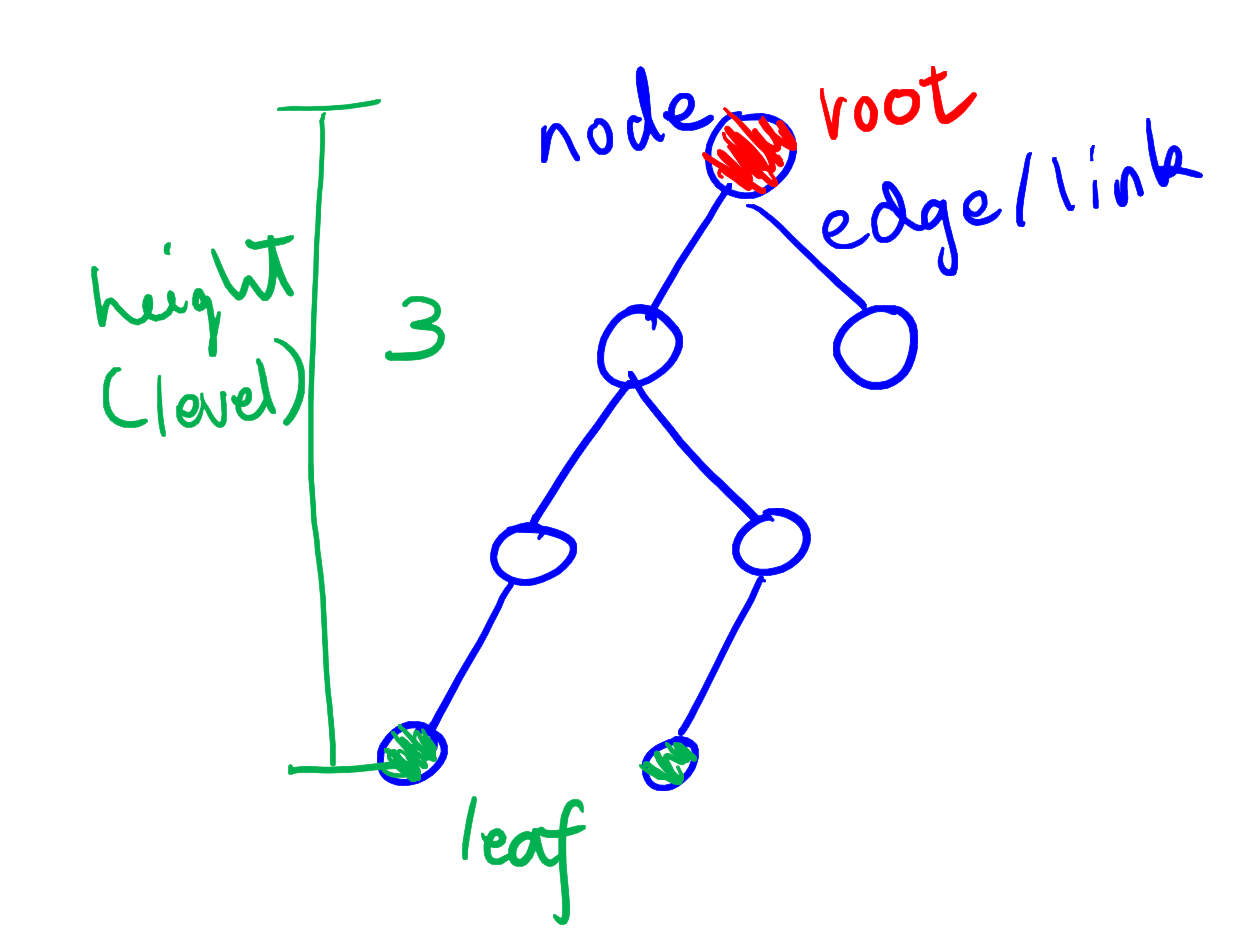
关于二叉树有以下几个概念：

• 二叉树：二叉树的节点包括它携带的数据、left（对左子节点的引用）和 right（对右子节点的引用）。换句话说，二叉树里的每个节点最多只有两个子节点。
• 满二叉树：每个节点只有 0 个或 2 个节点。
• 完全二叉树：一棵每一行从左到右都完全具有节点的二叉树，最底一行可以例外，但也必须从左到右不能有间隔。
• 二叉搜索树：对于每个有键 k 的节点，它的左子树里的每个节点的键都必须小于 k，而它右子树里的每个节点的键都必须大于 k（不允许重复键）。

实现

这里实现的是二叉搜索树。首先实现基本数据结构和节点的数据结构：

class BinarySearchTree<K: Comparable, V> {

    class Node<K: Comparable, V>: Equatable {

        let key: K
        let value: V
        var left: Node<K, V>?
        var right: Node<K, V>?

        init(key: K,
             value: V,
             left: Node<K, V>? = nil,
             right: Node<K, V>? = nil) {
            self.key = key
            self.value = value
            self.left = left
            self.right = right
        }

        // Implement equatable protocol for node
        static func == (lhs: Node<K, V>,
                        rhs: Node<K, V>) -> Bool {
            return lhs.key == rhs.key
                && lhs.left == rhs.left
                && lhs.right == rhs.right
        }
    }

    private(set) var root: Node<K, V>?

    init(root: Node<K, V>? = nil) {
        self.root = root
    }

}

搜索方法根据 binary search tree 的特性实现，复杂度为 O(log n)。

func search(key: K) -> Bool {
    guard root != nil else {
        return false
    }

    var current = root
    while current?.key != key {
        if current == nil {
            return false
        }
        if current!.key < key {
            current = current?.right
        } else {
            current = current?.left
        }
    }
    return true
}

要插入一个节点，首先还是需要搜索到节点在树中的位置，然后通过修改引用插入到树中。

func insert(key: K, value: V) {
    let newNode = Node(key: key, value: value)
    if root == nil {
        root = newNode
        return
    }

    var parent = root
    var current = root

    while true {
        if current?.key == key {
            return
        }
        parent = current
        if current != nil && current!.key < key {
            current = current!.right
            if current == nil {
                parent?.right = newNode
                return
            }
        } else {
            current = current?.left
            if current == nil {
                parent?.left = newNode
                return
            }
        }
    }
}

而要删除一个节点，我们需要分别考虑以下几种情况：

• 要删除的节点不在树中
• 要删除的节点是叶节点
• 要删除的节点有一个子节点
  • 只有左子节点
  • 只有右子节点
• 要删除的节点有两个子节点

首先搜索到节点：

func delete(key: K) {
    if root == nil {
        return
    }

    var parent = root
    var current = root
    var isLeftChild = false

    // find the current node
    while current != nil, current?.key != key {
        parent = current
        if current != nil && current!.key > key {
            isLeftChild = true
            current = current!.left
        } else {
            isLeftChild = false
            current = current?.right
        }
    }

    // TODO:
}

我们考虑节点未找到的情况：

// case 1: node not found
guard let current else {
    return
}

接下来考虑节点是一个叶节点（即没有子节点），如果该节点是父节点的左子节点，则直接将父节点的左子节点设为 nil，否则把右子节点置空。

// case 2: a leaf
if current.left == nil && current.right == nil {
    if current == root {
        root = nil
        return
    }
    if isLeftChild {
        parent?.left = nil
    } else {
        parent?.right = nil
    }
}

然后考虑节点只有一个子节点的情况：如果该节点是父节点的左子节点，则将父节点的左子节点设为自己的子节点；否则将父节点的右子节点设为自己的子节点。

// case 3: one child
// only has left child
else if current.right == nil {
    if current == root {
        root = current.left
        return
    }
    if isLeftChild {
        parent?.left = current.left
    } else {
        parent?.right = current.left
    }
}

最后考虑节点具有两个子节点的情况。这时我们不能简单地更改引用了，我们需要找到这个节点的“继任者”，来代替被删除的节点在树中的位置。一般来说，继任者节点就是在待删除节点右子树中具有最小 key 的节点。我们首先实现寻找继任者的函数：

private func getSuccessor(toDelete: Node<K, V>) -> Node<K, V>? {
    // find the minimum node in toDelete's right subtree
    var parent: Node<K, V>? = toDelete
    var successor: Node<K, V>? = toDelete
    var current = toDelete.right

    while current != nil {
        parent = successor
        successor = current
        current = current?.left
    }

    if successor != toDelete.right {
        parent?.left = successor?.right
        successor?.right = toDelete.right
    }

    return successor
}

有了这个函数，我们继续实现删除函数中的第四种情况：

// case 4: two children
else {
    let successor = getSuccessor(toDelete: current)
    if current == root {
        root = successor
        return
    }
    if isLeftChild {
        parent?.left = successor
    } else {
        parent?.right = successor
    }
    successor?.left = current.left
}

遍历

对于树的遍历一般有三种：

• Inorder：遍历顺序为 left -> parent -> right
• Preorder：顺序为 parent -> left -> right
• Postorder：顺序为 left -> right -> parent

DFS

遍历二叉树最常用的就是深度优先搜索和广度优先搜索，Inorder DFS 遍历可以通过递归简单地实现：

func dfsTraverse() -> [Node<K, V>] {
    var res: [Node<K, V>] = []
    traverse(node: root, res: &res)
    return res
}

// traversal helper function
private func traverse(node: Node<K, V>?, res: inout [Node<K, V>]) {
    guard let node else {
        return
    }
    traverse(node: node.left, res: &res)
    res.append(node)
    traverse(node: node.right, res: &res)
}

Preorder 和 Postorder 仅需要交换最后三行代码的顺序即可，不做赘述。

BFS

广度优先搜索的中心思想就是从根节点开始沿着树的宽度遍历树的节点，一般会用一个 Queue 来保持所有展开的节点。一个简单的实现如下：

func bfsTraverse() -> [Node<K, V>] {
    guard let root else {
        return []
    }
    var queue = [root]
    var ret: [Node<K, V>] = []
    var index = 0
    while index < queue.count {
        let node = queue[index]
        ret.append(node)
        if let left = node.left {
            queue.append(left)
        }
        if let right = node.right {
            queue.append(right)
        }
        index += 1
    }
    return ret
}

Iterative

Iterative 的遍历就比较有意思了，通常是利用一个栈来模拟 DFS 递归调用的过程。

Inorder

保持一个 Stack，循环：

• 寻找树的最左边节点，一路上所有的元素都入栈
• 出栈，访问节点
• 如果这个节点存在右子树，回到第一步（即寻找右子树的最左边节点，一路上所有元素都入栈）

直到栈变成空，表示我们已经访问过了所有的元素。

Inorder iterative 的实现如下：

func inorderTraverse() -> [Node<K, V>] {
    guard let root else {
        return []
    }
    var stack: [Node<K, V>] = []
    var res: [Node<K, V>] = []
    var current: Node<K, V>? = root
    while current != nil || !stack.isEmpty {
        // add all through the left-most node of the tree
        while current != nil {
            stack.append(current!)
            current = current!.left
        }
        current = stack.popLast()
        if current != nil {
            res.append(current!)
        }
        // if the removed node still has non-empty right subtree,
        // add all through the right node's left most child
        current = current?.right
    }
    return res
}

Preorder

保持一个 Stack，初始化为 [root]，循环：

• 出栈，访问节点
• 如果有右子树，入栈
• 如果有左子树，入栈

注意：由于栈后入先出的特性，这里入栈的顺序（先右再左）和访问的顺序（先左再右）相反。

实现：

func preorderTraverse() -> [Node<K, V>] {
    guard let root else {
        return []
    }
    var stack = [root]
    var res: [Node<K, V>] = []
    while !stack.isEmpty {
        guard let current = stack.popLast() else {
            break
        }
        res.append(current)
        if let right = current.right {
            stack.append(right)
        }
        if let left = current.left {
            stack.append(left)
        }
    }
    return res
}

Postorder

后序遍历可以仿照前序遍历的写法，不同的是我们可以构造一个按 parent -> right -> left 访问的顺序，然后把遍历结果反转过来即可得到后序遍历结果。

实现：

func postorderTraverse() -> [Node<K, V>] {
    guard let root else {
        return []
    }
    var stack = [root]
    var res: [Node<K, V>] = []
    while !stack.isEmpty {
        guard let current = stack.popLast() else {
            break
        }
        // to avoid extra reverse, just insert at 0
        res.insert(current, at: 0)
        // access: right -> left, push into stack: left -> right
        if let left = current.left {
            stack.append(left)
        }
        if let right = current.right {
            stack.append(right)
        }
    }
    return res
}

Heap

堆是一类基于树的特殊的数据结构，通常我们反复从堆中提取一个最大值或最小值，这里我们以最大堆 Max Heap 为例。最大堆是一个二叉树，且具有以下性质：

• （几乎是）完全二叉树：除最底层外，每一层的树都从左到右完全具有节点
• 最大值在树的根节点
• 最大堆的每个节点的子树都小于它

堆不是一个排好序的数据结构，而是可以被看作部分有序。堆的高度为 log(n)。一个最大堆的主要操作是 insert() 和 removeMax()（最小堆就是 removeMin()），后面会详解。

基于数组的实现

由于堆是（几乎）完全二叉树的性质，我们可以利用一个数组实现堆。对一个（几乎）完全二叉树，可以对每个元素从左到右、从上到下从 1 开始编号：

可以发现规律：每个节点的左子节点编号是它的编号的二倍，右子节点的编号是它编号二倍加一。利用这个规律，我们可以推出数组下标（从 0 开始）的关系：

• parent = (index - 1) / 2
• leftChild = index * 2 + 1
• rightChild = (index + 1) * 2

class MaxHeap<T: Comparable> {

    class Node<T> {
        let key: T
        init(key: T) {
            self.key = key
        }
    }

    private var heapArray: [Node<T>]

    init() {
        self.heapArray = []
    }

}

Insert

向最大堆插入元素的算法如下：

• 把新的数据插入到堆的下一个节点，使堆保持（几乎）完全二叉树结构。一般来说如果最后一层不满就往右边插入，最后一层满了就插到下一行的最左边
• 比较新节点和父节点，如果新节点较大，则把新的节点和它的父节点交换。重复这个过程，直到整个树满足堆的条件

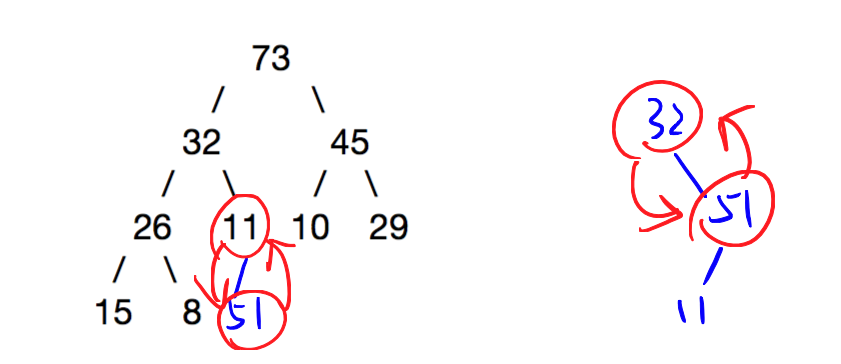
// insert into MaxHeap
func insert(_ key: T) {
    let node = Node(key: key)
    heapArray.append(node)
    percolateUp(index: heapArray.count - 1)
}

// percolate up helper function
private func percolateUp(index: Int) {
    // save the bottom node
    guard let bottom = heapArray.last else {
        return
    }
    var index = index
    // find the initial index value of parent
    var parent = (index - 1) / 2
    // while parent's key is smaller than the new key
    while index > 0 && heapArray[parent].key < bottom.key {
        // parent node comes down
        heapArray[index] = heapArray[parent]
        // index moves up
        index = parent
        // continue with its parent
        parent = (parent - 1) / 2
    }
    // finally, insert newly added node into proper position
    heapArray[index] = bottom
}

RemoveMax

从最大堆移除最大元素的算法如下：

• 移除掉根节点（就是最大的元素）并把整个树最底层的节点替换到根的位置，以使堆保持完全二叉树结构
• 如果这个节点比它的较大的子节点小，则交换它们；重复这个过程直到整个树满足堆的条件

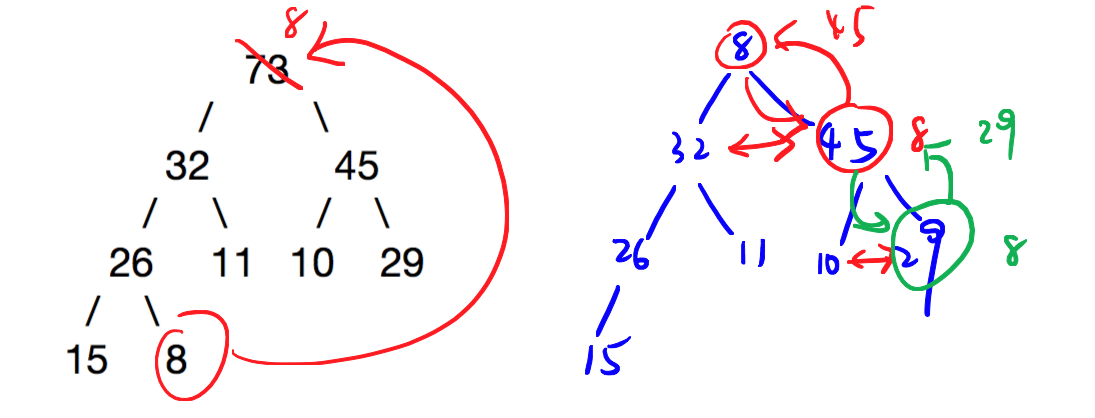
// remove max from heap
func removeMax() -> Node<T>? {
    guard let root = heapArray.first else {
        return nil
    }
    if let last = heapArray.last {
        heapArray[0] = last
        heapArray.removeLast()
    }
    if !heapArray.isEmpty {
        perculateDown(index: 0)
    }
    return root
}

// perculate down helper function
private func perculateDown(index: Int) {
    var index = index
    let top = heapArray[index]
    // index of larger child
    var largerChild = -1
    while index < heapArray.count / 2 {
        let leftChild = index * 2 + 1
        let rightChild = (index + 1) * 2
        // find which child is larger
        if rightChild < heapArray.count,
            heapArray[leftChild].key < heapArray[rightChild].key {
            largerChild = rightChild
        } else {
            largerChild = leftChild
        }
        // no need to go down any more
        if heapArray[largerChild].key < top.key {
            break
        }
        // move the nodes up
        heapArray[index] = heapArray[largerChild]
        // index goes down towards larger child
        index = largerChild
    }
    // put top key into proper location to restore the heap
    heapArray[index] = top
}

堆排序和优先队列

堆排序是一种非常有趣的排序方法，基本思路就是从未排序的数组一个个把元素丢到堆里，然后再一遍遍 removeMax() 或 removeMin()，就得到了排好序的数组。插入和移除操作的 worst-case 都是 O(n log n)。

func heapSort(data: [Int]) -> [Int] {
    let heap = MaxHeap<Int>()
    for i in data {
        heap.insert(i)
    }
    var ret: [Int] = []
    for _ in 0 ..< data.count {
        if let max = heap.removeMax() {
            ret.insert(max.key, at: 0)
        }
    }
    return ret
}

在 Java Collections 框架的实现中，PriorityQueue 类就是使用最小堆实现的。因此，遍历一个优先队列不能保证元素的顺序（因为堆是部分有序的），必须要一个个出队才能获得正确的顺序。

小结

以上就是几种基础的数据结构和它们的简单实现。不同数据结构由于设计和实现的不同，在看似相同的方法背后有着截然不同的原理和复杂度。在日常开发过程中，一定要根据业务需求选择合适的数据结构，合理利用系统资源，提高总体运行效率。